特性とは、目的とする品質（目的変数や Y）に期待している性質のことです。 品質工学では、対象にしている品質について、特性の違いを考慮しています。
特性の違いの考慮の仕方ですが、 具体的には、特性の種類によってSN比の計算式が異なっています。 （ 静特性のSN比、 動特性のSN比 を参照）
特性は、静特性と動特性に大きく分かれます。 静特性に分類される特性については、数理的な違いは、SN比の計算式だけです。 静特性と動特性の違いは、SN比の計算式もそうですが、 もっと根本的なところが違います。
Yの目標値が、特定の値を想定している特性です。 特定の値の目指す性質によって、分類されています。
平均の大きさがばらつきに影響しない特性
（平均値が一定値であることが目標になっている場合で、
必ずしも、その一定値がゼロでなくて良いです。）
平均の大きさがばらつきに影響する特性
（平均が大きくなると、ばらつきも大きくなる性質がある時、平均が大きくなった分の効果を差し引く必要があります。）
品質の値が、負の値ではなく、０を目標値とする特性 （小さければ小さいほど良い場合。ただし、マイナスになってはダメ）
０よりも大きな値のすべてがばらつきと考えられる場合が、望小特性です。 別の言い方をすると、０よりも大きな値として測定されているものは、有害・不利益を表す値の場合です。
有害・不利益を表す値なら、何でも望小特性になる訳ではなく、ばらつきのような性質のもの、いくつになるのかが予測できないような性質のものが、 望小特性になります。 これに当てはまらない場合は、小さければ小さいほど良いものだとしても、望目特性やゼロ望目特性として扱う方が適切です。
品質の値が、負の値ではなく、無限大を目標値とする特性 （大きければ大きいほど良い場合）
望小特性とは逆で、ばらつきが大きいほど、良い事になる場合です。
ただし、望小特性と同様に、ばらつきのような性質のもの、いくつになるのかが予測できないような性質のものです。 これに当てはまらない場合は、大きければ大きいほど良いものだとしても、望目特性やゼロ望目特性として扱う方が適切です。
目的とする機能が得られる値に範囲があって、 範囲が広いほど良いとされる特性です。 範囲の上側を望大特性、下側を望小特性と解釈し、 望大特性と望小特性のSN比を同時に最適化することを狙います。
動特性とは、X（信号因子）によって、Yが変化する特性のことです。 実際的な言い方をすると、X を変化させることによって、 Y も変化するような現象を品質にしているケースが当てはまります。 例えば、車のブレーキの品質は、動特性です。 これは、踏み込む量（X）と、ブレーキの効き具合（Y）の関係があります。
「動特性が良い」とは、Xの値が変化しても、 それぞれのXの値に対して、期待するYの値が、確実に得られることを言います。 ブレーキの例で言えば、同じように踏み込んでもブレーキの効き具合が、 その時その時で違ったら危険なので、XとYの確実な数値関係が望まれます。 動特性の実験では、 制御因子と誤差因子の組合せ条件の中で、 「動特性が良い」条件を探します。
品質工学 の文献では、動特性は３種類とされることがあります。（ 詳しくは 動特性のSN比の歴史 のページに書きました。）
筆者は、下記のように８種類に分けました。 ２×２×２で８種類です。 「等分散・比例分散」で２種類に分かれます。 「分散が傾きに比例する・しない」で２種類です。 「原点が基準・基準ではない」で２種類です。
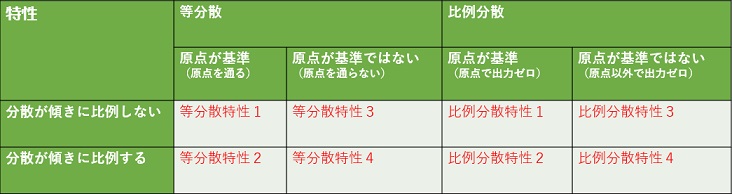
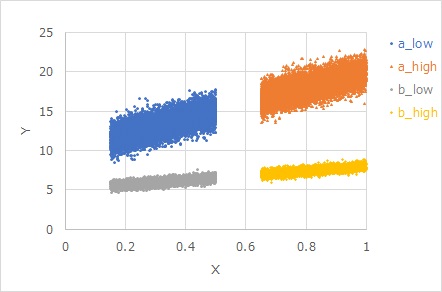
下のグラフの見方ですが、それぞれの特性を仮定した場合は、図の中の４つのグループは、「ばらつきの大きさが同じ」となります。
等分散というのは、Xに比例してYは増えますが、Xの値が同じ時のYのばらつき方は、一定と仮定できる場合です。
太さが一定の帯の上に、分布があるイメージです。
「分散が傾きに比例しない」というのは、異なる傾きの分布が２つあった時に、それらの帯のY軸方向の長さは、一定なのが自然と考えられる場合です。
等分散特性１の意味では、上図の４つのグループは「ばらつきの大きさが同じ」とみなします。
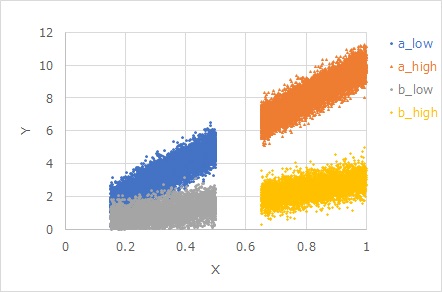
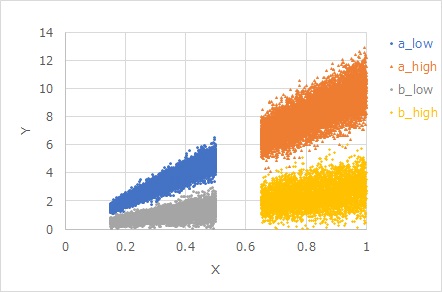
同じ等分散でも、「分散が傾きに比例する」の場合は、傾きが２倍になると、帯の幅も２倍になるのが自然と考えられる場合です。
見た目だと、傾きが緩い方が、帯の幅が狭く見えていたとしても、「分散が傾きに比例する」という性質があるのなら、「ばらつきの大きさが同じ」となることがあります。
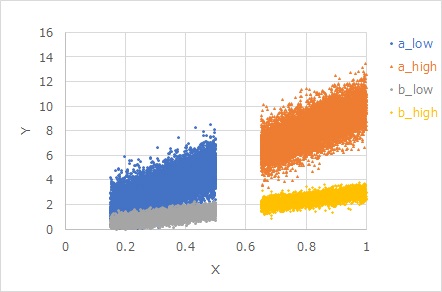
等分散特性１の応用です。
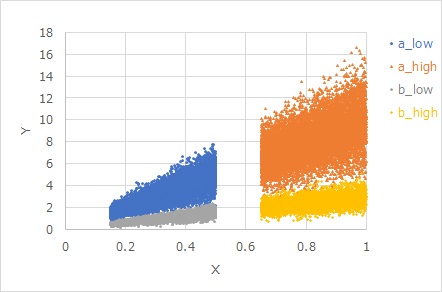
等分散特性で、「原点が基準ではない」というのは、原点を通らない場合です。
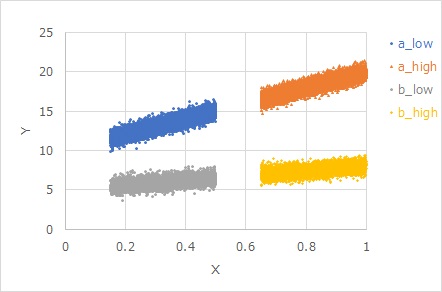
等分散特性２の応用で、原点を通らない場合です。
「比例分散」というのは筆者の造語です。
等分散と違って、Xに比例してばらつきの大きさが変わります。
このサイトでは、「比例分散」と呼んでいます。
「分散が傾きに比例しない」というのは、異なる傾きの分布が２つあった時に、同じXなら、２つの分布のばらつきが同じなのが、自然と考えられる場合です。
等分散特性２と同じように、比例分散特性でも分散が傾きに比例する場合が考えられます。
このサイトでは、
「比例比例分散モデル」と呼んでいます。
比例分散特性３・４は、比例分散特性１・２で、原点が基準ではない場合が対応します。
ただ、比例分散というのは、原点から分散が広がることに本質的な意味があるので、原点以外から広がる物理現象は、考えにくいです。
「ベーシック 品質工学へのとびら」 田口玄一・横山巽子 共著 日本規格協会 2007
ゼロ望目特性の例：反り
望小特性の例：排ガス
望大特性の例：強度
「オフライン品質工学の展望（3）」 品質工学会7
https://www.rqes.or.jp/library/basicKnowledge/offlineQe/offlineQe3.html
望小特性の例：摩耗量、偏芯、曲がり
望大特性の例：増幅率、出力、強さ、収量
順路
次は
静特性と動特性の違い
